MrLavaLoba: A new probabilistic model for the simulation of lava flows as a settling process
de’ Michieli Vitturi M., S. Tarquini (2017)
Journal of Volcanology and Geothermal Research, https://doi.org/10.1016/j.jvolgeores.2017.11.016, in press.
Introduction
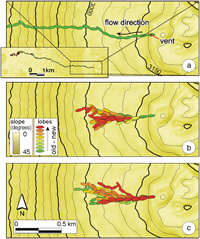
Forecasting lava flow emplacement is a critical issue atmany basaltic volcanoes where the propagation of flowing lavas threaten surrounding properties and infrastructures. Lava flow simulation is becoming an important tool for hazard and risk assessment before and during ongoing eruptions (Favalli et al., 2009a, 2009b; Cappello et al., 2016; Cordonnier et al., 2016; Richter et al., 2016; Dietterich et al., 2017). Existing numerical codes for the simulation of lava flow emplacement are either so-called deterministic codes based on the solution of some simplification of the physical governing equations of this phenomenon (Hidaka et al., 2005; Del Negro et al., 2008; Crisci et al., 2010), or, instead, so-called probabilistic codes based on the simple evidence that lava flows tend to follow the steepest descent path downhill (Macedonio et al., 1990; Felpeto et al., 2001; Favalli et al., 2005). Deterministic codes attempt tomimic,with a sufficiently accurate approximation, the thermo- and/or fluid-dynamics of the natural system, so that the emplacement of the erupted volume over time can be derived if input parameters are set to the correct values. Probabilistic codes instead give more emphasis to the uncertain character of the solution (Gilbert and Sparks, 1998) because the parameters and the processes under examination are known only imprecisely (e.g. with respect to the effusion rate, Harris et al., 2007). Deterministic simulations, in principle, provide a final coverage and thickness of lava flow field as well as detailed information of the lava flow emplacement over time, including the velocity of advancement of the front and the overall shape and thickness of the final flow field (Vicari et al., 2011). The output of a probabilistic simulation typically provides the most likely path of the flow and the associated inundated area, without constrain on the thickness of the final flow field nor temporal insight into the planimetric evolution of the lava flow (Tarquini and Favalli, 2013, 2016; Mossoux et al., 2016). Glaze and Baloga (2013) recently developed and Hamilton et al. (2013) tested a newcodewhichwas specifically focused on the simulation of late-stage pahoehoe lobes where random processes dominate emplacement (Baloga and Glaze, 2003; Glaze and Baloga, 2013). This code can be considered probabilistic because the approach for selecting the transfer direction (North, South, East orWest) is based on the generation of a randomnumber. In contrastwith earlier probabilistic codes, this code can provide as output the volume of the emplaced lava over time (i.e. the supply rate). This approach utilizes erupted volumes, one of the most critical input parameters considered by deterministic codes, within the stochastic approach of probabilistic codes. This allows for properties of the lava field, such as final thickness, to be addressed through a probabilistic approach. In this paper, a newprobabilistic code to simulate lava flows ispresented. This code, named MrLavaLoba, rests on an approach similar to the one introduced by Glaze and Baloga (2013). Substantial differences are introduced, such as taking into account the topography and removing the limitation of only four transport directions allowed.We test MrLavaLoba for the simulation of the emplacement of pahoehoe and channel-fed ‘a‘ā lava flows, and we show that, through the tuning of input parameters, the model can provide solutions for coverage area and thickness.
https://www.sciencedirect.com/science/article/pii/S0377027311001193