de’ Michieli Vitturi M., T. Esposti Ongaro, G. Lari, and A. Aravena (2019).
Geoscientific Model Development, 12, 581-595, https://doi.org/10.5194/gmd-12-581-2019.

Abstract

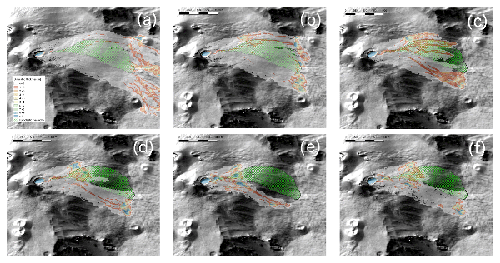
Pyroclastic avalanches are a type of granular flow generated at active volcanoes by different mechanisms, including the collapse of steep pyroclastic deposits (e.g., scoria and ash cones), fountaining during moderately explosive eruptions, and crumbling and gravitational collapse of lava domes. They represent end-members of gravity-driven pyroclastic flows characterized by relatively small volumes (less than about 1 Mm3) and relatively thin (1–10 m) layers at high particle concentration (10–50 vol %), manifesting strong topographic control. The simulation of their dynamics and mapping of their hazards pose several different problems to researchers and practitioners, mostly due to the complex and still poorly understood rheology of the polydisperse granular mixture and to the interaction with the complex natural three-dimensional topography, which often causes rapid rheological changes. In this paper, we present IMEX_SfloW2D, a depth-averaged flow model describing the granular mixture as a single-phase granular fluid. The model is formulated in absolute Cartesian coordinates (whereby the fluid flow equations are integrated along the direction of gravity) and can be solved over a topography described by a digital elevation model. The numerical discretization and solution algorithms are formulated to allow for a robust description of wet–dry conditions (thus allowing us to accurately track the front propagation) and an implicit solution to the nonlinear friction terms. Owing to these features, the model is able to reproduce steady solutions, such as the triggering and stopping phases of the flow, without the need for empirical conditions. Benchmark cases are discussed to verify the numerical code implementation and to demonstrate the main features of the new model. A preliminary application to the simulation of the 11 February pyroclastic avalanche at the Etna volcano (Italy) is finally presented. In the present formulation, a simple semi-empirical friction model (Voellmy–Salm rheology) is implemented. However, the modular structure of the code facilitates the implementation of more specific and calibrated rheological models for pyroclastic avalanches.